相机模型(针孔相机模型)
针孔相机模型的介绍
相机模型如图,有相机中心(针孔)、图像平面(这个是等价的图像平面)、焦距f、物理世界的真实的一点P

相机模型的作用就是我们对于物理世界拍照的时候,物理世界的每个点会落在我们拍出来的照片的哪个像素上。
一共有4个坐标系:世界坐标系(随便定义的一个坐标系,可以描述物理世界的任意一个点的坐标,是最大的坐标系)、相机坐标系(如图以相机中心C为原点的坐标系)、图像坐标系(如图以图像中某一点O为原点的坐标系)和像素坐标系(以图像平面的左上角为原点,且每个点都是整数坐标因为是像素的坐标系)
针孔相机模型就是推导4个坐标系之间的坐标转换。
使用针孔相机模型的流程是:
一开始要先对物理世界随便建个坐标系也就是世界坐标系,这样物理世界每个点都有坐标
然后对任一点,求出它在相机坐标系里的坐标。相机坐标系会相对世界坐标系旋转和平移,因为我们拍照的时候,相机会相对物理世界运动
然后根据相机坐标系的坐标,求出图像坐标系的坐标
然后根据图像坐标系的坐标,求出像素坐标系的坐标
世界坐标系\(\rightarrow\)相机坐标系
无论相机怎么移动、旋转,相机坐标系相对于世界坐标系只是做了一次刚体变换
一次欧式变化可以拆成一次旋转和一次平移,而经过推导,最终可以把一次刚体变换变成一次矩阵乘法
假设我们知道一个坐标系的基\((\vec{e_1},\vec{e_2},\vec{e_3})\)、另一个坐标系的基\((\vec{e_1'},\vec{e_2'},\vec{e_3'})\),这2个坐标系只有旋转而没有平移也就是原点是一个点,那么对于一个向量,它的坐标满足如下等式: \[ \begin{bmatrix}\vec{e_1},\vec{e_2},\vec{e_3}\end{bmatrix}\begin{bmatrix}a_1 \\ a_2 \\ a_3\end{bmatrix}=\begin{bmatrix}\vec{e_1'},\vec{e_2'},\vec{e_3'}\end{bmatrix}\begin{bmatrix}a_1' \\ a_2' \\ a_3'\end{bmatrix} \] 同时左乘\(\begin{bmatrix}\vec{e_1^T}\\ \vec{e_2^T} \\ \vec{e_3^T}\end{bmatrix}\),因为e都是单位正交向量,所以左边变成了单位矩阵,结果是: \[ \vec{a}=\begin{bmatrix}a_1 \\ a_2 \\ a_3\end{bmatrix}=\begin{bmatrix}\vec{e_1^T}\vec{e_1'} & \vec{e_1^T}\vec{e_2'} & \vec{e_1^T}\vec{e_3'} \\ \vec{e_2^T}\vec{e_1'} & \vec{e_2^T}\vec{e_2'} & \vec{e_3^T}\vec{e_3'} \\ \vec{e_3^T}\vec{e_1'} & \vec{e_3^T}\vec{e_2'} & \vec{e_3^T}\vec{e_3'} \end{bmatrix}\begin{bmatrix}a_1' \\ a_2' \\ a_3'\end{bmatrix}\overset{def}{=}R\vec{a'} \] R就是我们要的旋转矩阵。
如果只有旋转,没有平移,那么我们用世界坐标系的基和相机坐标系的基一算,就有了R,对于世界坐标系里的任意一点的坐标\(a'=\begin{pmatrix}a_1' \\ a_2' \\ a_3'\end{pmatrix}\),我们用R和它一乘,就有了相机坐标系的坐标\(a=\begin{pmatrix}a_1 \\ a_2 \\ a_3\end{pmatrix}\)
加上平移很简单,对于世界\(\rightarrow\)相机这一变换,有2种写法
第1种是学习针孔相机模型时常见的写法,如下 \[ \begin{bmatrix}\vec{a'} \\ 1 \end{bmatrix}=\begin{bmatrix}R & t \\ 0^T & 1\end{bmatrix}\begin{bmatrix}\vec{a} \\ 1\end{bmatrix}\overset{def}{=}T\begin{bmatrix}\vec{a} \\ 1\end{bmatrix} \] 第2种是后面学习PnP中的DLT时的写法,如下 \[ \vec{a'}=\begin{bmatrix}R|t\end{bmatrix}_{3\times 4}\begin{bmatrix}\vec{a}\\1\end{bmatrix} \] 其实是一样的,下面的相机\(\rightarrow\)图像这一变换就是普通坐标而不是齐次坐标了,所以我认为第1种写法只是为了搞出外参矩阵,第2种写法是方便把整个变换写成1个式子
所以回到世界坐标系\(\rightarrow\)相机坐标系,我们需要有世界坐标系的基、相机坐标系的基,这样可以求出旋转矩阵R,还需要世界坐标系的原点位置、相机坐标系的原点位置,这样可以求出平移向量t。这样T就可以求出。然后对于世界坐标系的任意一点,给出坐标就能求出在当前相机的位置和位姿下,它在相机坐标系的坐标,如下式 \[ P_{camera}=TP_{world} \]
相机坐标系\(\rightarrow\)图像坐标系
回到针孔相机模型图

图中蓝色三角形和橙色三角形相似,所以有下式(注意相机坐标系是三维的,而图像坐标系是二维的,就那一个面) \[ \begin{align}& \frac{Z}{f}=\frac{X}{x}=\frac{Y}{y} \\ \overset{}{\Rightarrow} &x=f\frac{X}{Z},y=f\frac{Y}{Z}\end{align} \] 所以得到了图像坐标系下的坐标\((x,y)\)
图像坐标系\(\rightarrow\)像素坐标系
图像坐标系的原点一般是不一定在哪,比如图中是在照片的中间,而像素坐标系的原点一般规定在左上角
图像坐标系的点的坐标是连续的,而像素坐标系是离散的
因此还需要把图像坐标系的坐标转到像素坐标系里
因为不同相机的像素点大小不同,所以同样是图像坐标系里的\((1,0)\),可能对于一个相机来说这个点会落在像素坐标系的\((1,0)\),而另一个相机的像素比较密,会落在\((10,0)\),也就是前面的单位都是米(或者厘米等长度单位),而到像素坐标系单位变成像素,所以会有一个缩放。再加上前面说的原点位置不同,有一个平移。因此是一个缩放+一个平移。
假设图像坐标系里的下标是\((x,y)\),像素坐标系里的下标是\((u,v)\),则满足下面关系,其中\(\alpha,\beta\)是缩放比例,\(c_x,c_y\)是平移。再结合相机坐标系\(\rightarrow\)图像坐标系,可以整理出结果 \[ \begin{aligned} &\left\{ \begin{aligned} u & =\alpha x+c_x \\ v & =\beta y+c_y \end{aligned} \right. \\ \overset{}{\Rightarrow} &\left\{ \begin{aligned} u & =f_x\frac{X}{Z}+c_x,其中f_x=f*\alpha \\ v & =f_y\frac{Y}{Z}+c_y,其中f_y=f*\beta \end{aligned} \right.\\ \overset{}{\Rightarrow} & \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} =\frac{1}{Z} \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \overset{def}{=} \frac{1}{Z}KP \end{aligned} \] 上式结果是,P是相机坐标系下的坐标,K被称为相机的内参数矩阵,Z是相机坐标系下的坐标Z,可以得到像素坐标系下的下标\((u,v)\)
再结合第一步世界坐标系\(\rightarrow\)相机坐标系,可以得到最后最后的结果: \[ \begin{align} P_{Camera}&=TP_{World}(齐次坐标) \\ ZP_{Pixel}&=KP_{Camera}(普通坐标) \end{align} \]
其中T就被称为相机的外参,随相机的旋转和平移而变换。K是内参。
如果合并为1个式子,从世界坐标系\(\begin{bmatrix}x\\y\\z\end{bmatrix}\)映射到像素坐标系\(\begin{bmatrix}u\\v\end{bmatrix}\),形式为 \[ \lambda \begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f_x&&c_x\\&f_y&c_y\\&&1\end{bmatrix}\begin{bmatrix}R|t\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix} \]
总结:
针孔相机模型的流程是:
给出世界坐标系的基、相机坐标系的基,求出R,然后给出世界坐标系的原点、相机坐标系的原点,求出t。用R和t拼出T。
给出焦距f,给出缩放比例\(\alpha,\beta\),求出\(f_x,f_y\),然后给出\(c_x,c_y\),拼出K
然后就可以对于任一点的世界坐标求出它落在哪个像素上
其中求出相机坐标系后,后续做的所有变换包括:(归一化平面)
- 把相机坐标系下的\(P_{camera}=[X,Y,Z]^T\)中的\(X,Y\)同除\(Z\)得到归一化平面
- \(X,Y\)同乘焦距\(f\)得到图像坐标
- 缩放+平移得到像素坐标
所以在对极几何中会遇到:
- 先有\(ZP_{pixel}=KP_{camera}\),并且\(Z\)是未知数,则\(KP_{camera}\)是\(P_{pixel}\)的未知数倍,就表示那条射线
- 再同乘\(K^{-1}\),\(K\)包含的就是焦距f、米到像素的缩放倍数\(\alpha,\beta\)、平移t,所以等于是把像素坐标还原到归一化平面(从相机坐标到像素坐标,分成除\(Z\)到归一化平面和乘\(K\)到像素坐标,现在乘\(K^{-1}\)就是回到归一化平面)
24/03/03总结
全程是在齐次坐标下运算的,\(P_{world},P_{camera}\)都是4维向量(\(P_{camera}\)就是世界坐标系转个位置),\(P_{image},P_{pixel}\)都是3维向量(都在平面上),归一化平面就是\(Z=1\)的时候算的那个坐标
下面右式每乘一个矩阵就变一步,看的这个。\(dX,dY\)表示一个像素的物理宽度和高度,\(f_x,f_y\)是\(\begin{aligned}f_x&=\frac{f}{dX}\\f_y&=\frac{f}{dY}\end{aligned}\) \[ Z\begin{pmatrix}u\\v\\1\end{pmatrix}=\underbrace{\begin{pmatrix}\frac{1}{dX}&0&u_0\\0&\frac{1}{dY}&v_0\\0&0&1 \end{pmatrix}\begin{pmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{pmatrix}}_{K}\underbrace{\begin{pmatrix}R&t\\0&1\end{pmatrix}}_{T}\begin{pmatrix}U\\V\\W\\1\end{pmatrix} \] 手动理清:
世界坐标系(\(\begin{pmatrix}U\\V\\W\\1\end{pmatrix}\)齐次坐标,4维)乘\(\begin{pmatrix}R&t\\0&1\end{pmatrix}\)得到相机坐标系(\(\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix}\),齐次坐标,4维)
相机坐标系(\(\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix}\),齐次坐标,4维)乘\(\begin{pmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{pmatrix}\)就是把\(X,Y\)缩放\(f\)倍得到图像坐标系(\(Z\begin{pmatrix}\frac{fX}{Z}\\\frac{fY}{Z}\\1\end{pmatrix}\),齐次坐标,3维)。也可以理解为,\(X,Y\)先缩\(\frac{1}{Z}\)倍得到归一化平面坐标,再扩\(f\)倍到成像平面上
相机坐标系(\(\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix}\),齐次坐标,4维)乘\(\begin{pmatrix}\frac{f}{Z}&0&0&0\\0&\frac{f}{Z}&0&0\\0&0&\frac{1}{Z}&0\end{pmatrix}\)得到像素坐标系(非齐次坐标,2维),或者像上图改为齐次坐标下的
图像坐标系(\(Z\begin{pmatrix}\frac{fX}{Z}\\\frac{fY}{Z}\\1\end{pmatrix}\),齐次坐标,3维)缩放+平移得到像素坐标系(\(Z\begin{pmatrix}u\\v\\1\end{pmatrix}\),齐次坐标,3维)
注!!!!
所以相机坐标系是包含了\(Z\)倍的,像素坐标系是不包含\(Z\)的,也就是\(Z\begin{pmatrix}u\\v\\1\end{pmatrix}=K\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix}\)。从相机坐标系转归一化平面只需\(X,Y\)缩\(\frac{1}{Z}\)倍,从像素坐标系转归一化平面乘\(\pmb{K}^{-1}\)即可
上面全程是齐次坐标,所以\(\pmb{K}\in \R_{4\times 4}\),但\(\pmb{K}\)第4列是全0。也可以改为非齐次坐标,把\(\pmb{K}\)第4列删了就行\(\pmb{K}\in \R_{3\times 4}\)
所以从世界坐标系到归一化坐标系可以用\([\pmb{R}|\pmb{t}]_{3\times 4}\)这种外参矩阵(因为\(\pmb{K}\)的第4列全是0)有\(s\begin{pmatrix}u\\v\\1\end{pmatrix}_{pixel}=[\pmb{R}|\pmb{t}]\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix}_{world}\)(PnP的DLT方法用到)
内参矩阵的齐次坐标\(\pmb{K}_{3\times 4}\)与非齐次坐标\(\pmb{K}_{3\times 3}\)对比:上面公式是齐次坐标表示\(\pmb{K}_{3\times 4}=\begin{pmatrix} \frac{f}{dX}&0&u_0&0\\0&\frac{f}{dY}&v_0&0\\0&0&1&0 \end{pmatrix}\),slam14讲书上是非齐次坐标表示\(\pmb{K}_{3\times 4}=\begin{pmatrix} f_x&0&c_x\\0&f_y&c_y\\0&0&1 \end{pmatrix}\),二者只是记号不同
畸变模型
有正径向畸变、负径向畸变、切向畸变,一般径向畸变的多
然后Brown提出了一个模型用于刻画这种畸变 \[ x''=x'\frac{1+k_1r^2+k_2r^4+k_3r^6}{1+k_4r^2+k_5r^4+k_6r^6}+2p_1x'y'+p_2(r^2+2x'^2)\\ y''=x'\frac{1+k_1r^2+k_2r^4+k_3r^6}{1+k_4r^2+k_5r^4+k_6r^6}+p_1(r^2+2y'2)+2p_2x'y' \] 里面的k,p都是常数
用法是,先用针孔相机模型算出来没畸变的像素位置,然后套这个公式求出了畸变的像素位置
张正友标定法
略
对极几何:2d-2d
前置知识
向量叉乘转换为矩阵:
计算向量的叉乘\(\vec{a}\times\vec{b}\),可以转化为矩阵乘法,如下式。其中\(\vec{a}^\wedge\)是a的反对称矩阵。 \[ \vec{a}\times\vec{b}=\begin{Vmatrix}\vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3\end{Vmatrix}=\begin{bmatrix}0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0\end{bmatrix}b\overset{def}{=}\vec{a}^{\wedge}\vec{b} \] 也就是2向量叉乘,可以变为一个的反对称矩阵和另一个向量做矩阵乘法。
齐次坐标下点在直线的充要条件:
考虑二维情况,一个点的齐次坐标是\(p^T=(x,y,1)\),一条直线是\(ax+by+c=0\)可以记作\(l:(a,b,c)\),则充要条件是二者点乘为0: \[ p^T\cdot l=0 \]
推导
终于推对了,放在齐次坐标下就对了
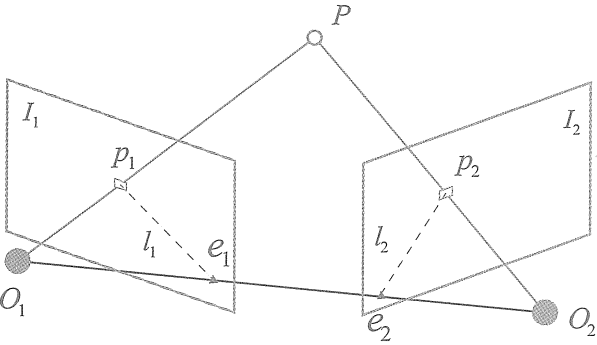
假设\(P\)在\(O_1\)的相机坐标系下的齐次坐标坐标为\(P=\begin{pmatrix}X\\Y\\Z\\ 1\end{pmatrix}\)
按照本文前面的针孔相机模型,假设内参为\(K_{3\times 4}\),外参为\(T_{4\times 4}\)(均为齐次坐标下的形状),则\(p_1=\begin{pmatrix}u_1\\v_1\\ 1\end{pmatrix},p_2=\begin{pmatrix}u_2\\v_2\\ 1\end{pmatrix}\)在各自平面\(I_1I_2\)的像素坐标系的齐次坐标满足 \[ \begin{aligned} &s_1p_1=KP\\ &s_2p_2=KTP \end{aligned} \] 其中\(s_1s_2\)是前面相机模型的Z,也就是以\(O_1\)为原点,作一个XYZ坐标系,XOY与\(I_1\)平行,\(\vec{O_1P}\)指向Z的正方向(而不是正轴,因为\(\vec{O_1P}\)可能不与\(I_1\)垂直),此时P点在这个坐标系里的z值就是\(s_1\)
因为\(s_1s_2\)都只是个常数,所以有 \[ \begin{aligned} &p_1\sim KP\\ &p_2\sim KTP \end{aligned} \] \(\sim\)表示左右成比例
令\(x_1=K^{-1}p_1,x_2=K^{-1}p_2\),两边同乘\(K^{-1}\)然后把\(x_1x_2\)代进去 \[ \begin{cases} x_1\sim P\\ x_2\sim TP \end{cases} \Rightarrow x_2\sim Tx_1 \] 两边左叉乘\(t\),再左乘\(x_2^T\) \[ x_2^T(t\times x_2)\sim x_2^T(t\times Tx_1) \] 会将左边变成0,则右边也是0。齐次坐标下是0,非齐次坐标下还是0(主要是不会对叉乘变形了),转到非齐次坐标下,注意下式的\(x_1,x_2\)都变成了非齐次坐标,所以\(T\)可以展开为\(R,t\)了 \[ x_2^T(t\times (Rx_1+t)) \] 展开,后一项变0,只剩下前一项,此时还是非齐次坐标 \[ \begin{aligned} &x_2^Tt^\wedge Rx_1=0\\ &p_2^TK^{-T}t^\wedge RK^{-1}p_1=0 \end{aligned} \] 最后结果是 \[ \begin{aligned} &E=t^\wedge R\\ &F=K^{-T}EK^{-1} \end{aligned} \] 如果2帧图像之间有若干个匹配点也就是已知\(p_1p_2\) or \(x_1x_2\),则可以求出E or F or R,t
或者已知\(p_1\),问右图的极线方程,按照齐次坐标的点在直线上的要求,\(p_2\)所在极线的方程是\(Fp_1\)
对极几何的缺点是尺度不确定和纯旋转
\(x_1x_2\)实际上是归一化平面上的\(\vec{O_1P},\vec{O_2P}\)的投影,归一化平面是前面\(s_1s_2\)那里建立的XYZ坐标系中z=1的平面,这个坐标系是针孔相机模型里最重要的坐标系了,平行于XOY的平面沿着Z轴平移,移到Z=1时就是归一化平面,移到Z=f时就是图像平面(tips因为\(\vec{O_1P}\)不一定与z轴重合所以\(p_1\)的z值只会\(\le f\))前面的针孔相机模型有\(ZP_{Pixel}=KP_{Camera}\),推导的时候\(Z\)就是f,但如果Z取1就求出了这个点在归一化平面的像素坐标了(\(1*p_1=Kx_1\)所以\(x_1x_2\)是归一化平面的像素坐标)
单应矩阵没看,这个视频的UP好像也讲了
opencv code
pose_estimation_2d2d(keypoints_1, keypoints_2, matches, R, t);这么算出来的\(R,t\)是\(x_2=Rx_1+t\)的(而不是反过来的)
三角测量
现在想要\(s_1s_2\)了,所以有公式 \[ s_2x_2=s_1Rx_1+t \] 两边左乘\(x_2^\wedge\),左边变成0,只剩右边 \[ s_1x_2^\wedge Rx_1+x_2^\wedge t=0 \] 可求出\(s_1\),同理可得\(s_2\)
opencv code
vector<Point3d> points;
triangulation(keypoints_1, keypoints_2, matches, R, t, points);三角测量的矛盾是,位移太小 or 图像分辨率太低(可能若干点投影到一个像素上)会导致精度低,但位移大外观可能变化大 or 提高分辨率会增加计算成本
PnP:3d_2d
DLT
已知一组3D点的世界坐标和它们在相机的相机坐标(或者说归一化平面坐标),求相机的位姿R,t。应用场景可以是相机的标定,也可以是相邻帧的位姿变化
假设一个3D点的世界坐标系的齐次坐标是\(P=\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix}\),投影到归一化平面的齐次坐标是\(\begin{pmatrix}u\\v\\1\end{pmatrix}\),则有 \[ \begin{aligned} s\begin{bmatrix}u\\v\\1\end{bmatrix}&=[R|t]\begin{bmatrix}X\\Y\\Z\end{bmatrix}=\begin{bmatrix}t_1&t_2&t_3&t_4\\t_5&t_6&t_7&t_8\\t_9&t_{10}&t_{11}&t_{12}\end{bmatrix}\begin{bmatrix}X\\Y\\Z\end{bmatrix} \end{aligned} \] 变形得到 \[ \begin{aligned} u=\frac{t_1X+t_2Y+t_3Z+t_4}{t_9X+t_{10}Y+t_{11}Z+t_{12}}\\ v=\frac{t_5X+t_6Y+t_7Z+t_8}{t_9X+t_{10}Y+t_{11}Z+t_{12}}\\ \end{aligned} \] 已知是\(u,v,X,Y,Z\),其他全未知,12个未知数需要6个3D点-2D点对
用归一化平面是假设已知内参K,但K未知也能做,多一些点即可
P3P
书上用三角形相似推出来方程组,然后方程组怎么解略了,那也不用看了
它是有4对(世界坐标系,像素坐标系)(3对算,1对验),用三角形相似推出方程组,然后解方程组得到相机坐标系的坐标,然后用3D-3D的方法解\(\pmb{R},\pmb{t}\)
BA
用李代数列出某个点的针孔相机模型,\(\pmb{P}_i\)是世界坐标系的齐次坐标,\(\pmb{u}_i\)是像素坐标系的齐次坐标,\(\pmb{K}\in \R_{3\times 4}\),\(\pmb{T}\in\R_{4\times 4}\) \[ s_i\pmb{u}_i=\pmb{K}\pmb{T}\pmb{P}_i \] 重投影误差是,用\(\pmb{P}_i\)和猜的\(exp(\pmb{\xi^\wedge})\)估计\(\pmb{u}_i\),与真实的\(\pmb{u}_i\)作差。最小化重投影误差 \[ \pmb{\xi}^*=\underset{\pmb{\xi}}{argmin}\frac{1}{2}\sum_{i=1}^n\parallel \pmb{u}_i-\frac{1}{s_i}\pmb{K}T\pmb{P}_i \parallel_2^2 \] 下面是推导:
复习高斯牛顿法:对于\(min_\pmb{x}\ F(\pmb{x})=\frac{1}{2}\parallel f(\pmb{x})\parallel_2^2\)可以一阶泰勒展开\(f(\pmb{x}+\Delta\pmb{x})\approx f(\pmb{x})+\pmb{J}(\pmb{x})^T\Delta\pmb{x}\),然后不断迭代
回到最小化重投影误差的式子,求解上式可以用高斯牛顿法。记$= _i-T_i \(对应高斯牛顿法的\)f\(,需要求出\)$
这里\(\pmb{e}\)是\(\pmb{T}\)的导数,李群不好求导,所以就换到李代数上用扰动模型求
注意\(\pmb{e}\)是估计的像素坐标和真实的像素坐标之差,齐次坐标下是3维的,只是第3维一直是0
设\(\pmb{T}=exp(\pmb{\xi}^\wedge)\),用扰动模型就是求\(\pmb{J}=\frac{\partial \pmb{e}}{\partial \delta\pmb{\xi}}\)。扰动模型是在非齐次坐标下推的,所以下面转换到非齐次坐标,设\(\pmb{P'}=\begin{pmatrix}X'\\Y'\\Z'\\1\end{pmatrix}\)是空间点\(\pmb{P}\)的相机坐标系的齐次坐标,则有链式法则 \[ \pmb{J}=\frac{\partial \pmb{e}}{\partial \pmb{P}'}\frac{\partial \pmb{P}'}{\partial \delta\pmb{\xi}} \] \(\pmb{P}'\)满足\(s\pmb{u}=\pmb{K}\pmb{P}'\)(仍然在齐次坐标下,书上是变成非齐次坐标了,但我自己一推发现没区别,所以是全程齐次坐标),因此有下列变换求出链式法则后的第1项(和书上比就是多了一圈0其他一样) \[ \begin{align} &\begin{pmatrix}su\\sv\\s\end{pmatrix}=\begin{pmatrix} f_x&0&c_x&0\\0&f_y&c_y&0\\0&0&1&0 \end{pmatrix}\begin{pmatrix}X'\\Y'\\Z'\\1\end{pmatrix}\\ \Rightarrow&\begin{cases} su=f_xX'+c_xZ'\\ sv=f_yY'+c_yZ'\\ s=Z' \end{cases}\\ \Rightarrow&\begin{cases} u=f_x\frac{X'}{Z'}+c_x\\ v=f_y\frac{Y'}{Z'}+c_y \end{cases}\\ \Rightarrow&\frac{\partial \pmb{e}}{\partial \pmb{P}'}=-\begin{pmatrix}\frac{\partial u}{\partial X'}&\frac{\partial u}{\partial Y'}&\frac{\partial u}{\partial Z'}&\frac{\partial u}{\partial 1} \\\frac{\partial v}{\partial X'}&\frac{\partial v}{\partial Y'}&\frac{\partial v}{\partial Z'}&\frac{\partial v}{\partial 1} \\ \frac{\partial 1}{\partial X'}&\frac{\partial 1}{\partial Y'}&\frac{\partial 1}{\partial Z'}&\frac{\partial 1}{\partial 1} \end{pmatrix}=-\begin{pmatrix}\frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}&0\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}&0\\0&0&0&0\end{pmatrix}_{3\times 4} \end{align} \] 前面推的扰动模型结果是\(\frac{\partial (\pmb{T}\pmb{p})}{\partial \delta\pmb{\xi}}=\begin{pmatrix}\pmb{I}&-(\pmb{R}\pmb{p}+\pmb{t})^\wedge\\0&0'\end{pmatrix}\)(前面李代数部分解释了这里就是齐次坐标的形式,所以现在还是在齐次坐标下)。相机坐标系是对世界坐标系进行了变换,和进行了扰动效果一样,所以\(\pmb{T}\pmb{p}=\pmb{P}'\),所以\(\pmb{R}\pmb{p}+\pmb{t}\)就相当于\(\pmb{P}'\)的前3维也就是非齐次坐标即\(\pmb{R}\pmb{p}+\pmb{t}=\begin{pmatrix}X'\\Y'\\Z'\end{pmatrix}\)
所以链式法则第2项结果为: \[ \frac{\partial \pmb{P}'}{\partial \delta\pmb{\xi}}=\begin{pmatrix}\pmb{I}&-\begin{pmatrix}X'\\Y'\\Z'\end{pmatrix}^\wedge\\0&0'\end{pmatrix}=\begin{pmatrix}1&0&0&0&Z'&-Y'\\0&1&0&-Z&0&X'\\0&0&1&Y'&-X'&0\\0&0&0&0&0&0\end{pmatrix}_{4\times 6} \] 合起来得到(和书上完全一样,除了因为齐次坐标而多出的一行0) \[ \pmb{J}=-\begin{pmatrix}\frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}&0\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}&0\\0&0&0&0\end{pmatrix}\begin{pmatrix}1&0&0&0&Z'&-Y'\\0&1&0&-Z&0&X'\\0&0&1&Y'&-X'&0\\0&0&0&0&0&0\end{pmatrix}=-\begin{pmatrix}\frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}&-\frac{f_xX'Y'}{Z'^2}&f_x+\frac{f_xX'^2}{Z'}&-\frac{f_xY'}{Z'}\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}&-f_y-\frac{f_yY'^2}{Z'^2}&\frac{f_yX'Y'}{Z'^2}&\frac{f_yX'}{Z'}\\0&0&0&0&0&0 \end{pmatrix} \] 大问题:书上把这个导数推出来就没了,我也不确定干啥用的,我猜的是,这个导数是配合高斯牛顿法迭代用?
\(\pmb{e}\)也可以看作是\(\pmb{P}\)的函数,找能让\(\pmb{e}\)最小的\(\pmb{P}\)就是优化特征点的空间位置。可以作如下推导 \[ \frac{\partial \pmb{e}}{\partial \pmb{P}}=\frac{\partial \pmb{e}}{\partial \pmb{P}'}\frac{\partial \pmb{P}'}{\partial \pmb{P}} \] 后面略了
code for EPnP
code运行不起来(g2o),所以纸上谈兵
// 假设有一组3d坐标pts_3d(vector<Point3f>类型)和一组2d坐标pts_2d((vector<Point2f>类型))一一对应
Mat r, t;
cv::solvePnP(pts_3d, pts_2d, K, Mat(), r, t, false);
Mat R;
cv::Rodrigues(r, R); // r为旋转向量形式,用Rodrigues公式转换为矩阵
cout << "R=" << endl << R << endl;
cout << "t=" << endl << t << endl;code for BA
前面推导的BA公式P186解释了,可以看到g2o库里求的Jacobian矩阵与推导的一样
代码略了,和g2o实现非线性最小二乘类似,先定义点和边,然后一连串固定代码。主要问题就是点和边在一个问题中是怎么确定的,但我找不到什么说法
PnP总结
一共介绍了DLT, P3P, BA,其中DLT和P3P相当于求出解析解所以只用了部分(3d,2d)点对,而BA是用所有的(3d,2d)点对做了非线性最小二乘(即使用了GaussNewton方法)所以会更准一些
BA的方法再具体一点,是用GaussNewton方法,一开始先选一个\(\pmb{T}\)作为初始值,然后用相机模型和3d点求出估计的2d点,最小化估计的2d点与实际的2d点的误差,迭代\(\pmb{T}\)
ICP:3D-3D
用2张RGBD图像进行特征匹配可以得到一组\((3d,3d)\)点对\(\pmb{P}=\{\pmb{p}_1,\pmb{p}_2,...\pmb{p}_n \}\ \& \ \pmb{P}'=\{\pmb{p}_1',\pmb{p}_2',...,\pmb{p}_n' \}\),ICP就是用\((3d,3d)\)点对求出一个\(\pmb{R},\pmb{t}\)
有2种解法,1是SVD,2是BA
SVD
类似重投影误差地定义出下面误差,使它最小 \[ J=\frac{1}{2}\sum_{i=1}^n\parallel (\pmb{p}_i-(\pmb{R}\pmb{p}_i'+\pmb{t})) \parallel_2^2 \] 经过一系列变换(很简单,一眼看完)得到 \[ \pmb{R}^*=\underset{\pmb{R}}{argmin} -tr(\pmb{R}\sum_{i=1}^n\pmb{q}_i'\pmb{q_i}^T) \] 其中\(\pmb{q}_i\)是\(\pmb{p}_i\)的去质心坐标即$_i=i-{i=1}^n_i $得到的
\(\pmb{t}\)跟着\(\pmb{R}\)变满足\(\pmb{t}^*=\pmb{p}-\pmb{R}\pmb{p}'\)所以只需要求出最佳的\(\pmb{R}\)就可以得到最佳的\(\pmb{t}\)
令\(\pmb{W}=\sum_{i=1}^n\pmb{q}_i\pmb{q}_i'^T\),则可以SVD分解\(\pmb{W}=\pmb{U}\pmb{\Sigma}\pmb{V}^T\)。若\(\pmb{W}\)满秩,则 \[ \pmb{R}=\pmb{U}\pmb{V}^T \] (为啥\(\pmb{R}\)这么求出来了不知道,书上也没说)所以是直接求出解析解
BA
类似PnP的方法,目标函数转到李代数上 \[ J=\frac{1}{2}\sum_{i=1}^n\parallel (\pmb{p}_i-exp(\pmb{\xi}^\wedge)\pmb{p}_i') \parallel_2^2 \] 则对\(\pmb{\xi}\)求导即可找到李代数层面的极小值
因为李群的乘法转到李代数的加法是近似的,所以需要迭代
书上还直接给出,ICP可以保证收敛到全局最优值
code for SVD
还是有g2o,没法运行了,但代码很简单。书上说opencv没有现成的用一组\((3d,3d)\)估计的,所以自己实现了一下
void pose_estimation_3d3d(const vector<Point3f> &pts1,const vector<Point3f> &pts2,Mat &R, Mat &t)
{
// 算质心
Point3f p1, p2; // center of mass
int N = pts1.size();
for (int i = 0; i < N; i++) {
p1 += pts1[i];
p2 += pts2[i];
}
p1 = Point3f(Vec3f(p1) / N);
p2 = Point3f(Vec3f(p2) / N);
// 算去质心坐标
vector<Point3f> q1(N), q2(N); // remove the center
for (int i = 0; i < N; i++) {
q1[i] = pts1[i] - p1;
q2[i] = pts2[i] - p2;
}
// 算W=q1*q2^T
Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
for (int i = 0; i < N; i++) {
W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z).transpose();
}
cout << "W=" << W << endl;
// 对W进行SVD分解
Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
Eigen::Matrix3d U = svd.matrixU();
Eigen::Matrix3d V = svd.matrixV();
cout << "U=" << U << endl;
cout << "V=" << V << endl;
// 得到R和t
Eigen::Matrix3d R_ = U * (V.transpose());
if (R_.determinant() < 0) {
R_ = -R_;
}
Eigen::Vector3d t_ = Eigen::Vector3d(p1.x, p1.y, p1.z) - R_ * Eigen::Vector3d(p2.x, p2.y, p2.z);
// convert to cv::Mat
R = (Mat_<double>(3, 3) <<
R_(0, 0), R_(0, 1), R_(0, 2),
R_(1, 0), R_(1, 1), R_(1, 2),
R_(2, 0), R_(2, 1), R_(2, 2)
);
t = (Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));
}